여러분, 안녕하세요! 오늘, 나는 가장 큰 일반적인 구분과 재미 있고 이해하기 쉬운 방식으로 가장 일반적인 배수의 관계에 대해 이야기 할 것입니다. 수학을 처음 만났을 때이 개념에 대해 혼란스러워 했습니까? 이 기사에서는 학습 과정을 단계별로 따라갈 수 있도록 쉽고 상세한 방식으로 둘 사이의 관계를 쉽고 상세하게 설명하려고 노력했습니다. 가장 큰 일반적인 제수와 가장 일반적인 배수는 무엇입니까? 먼저, GCD (Greatest Common Divisor)의 정의와 LCM (Lest Common Multiple)의 정의를 살펴 보겠습니다! GCD (Greatest Common Divisor) : 두 개 이상의 숫자의 가장 큰 공통 구분. 번호를 말하십시오. 예를 들어, 12와 18의 제수를 찾으면 12의 제수가 있고 18의 제수는 IS입니다. 이 중 공통의 구분은 가장 큰 공통 제수입니다. 가장 일반적인 다중 (LCM) : 두 숫자 또는 여러 숫자의 일반적인 배수 중 가장 작은 숫자를 나타냅니다. 예를 들어, 12와 18의 배수를 찾으면 12의 배수는 18 세의 배수입니다.이 중에서 가장 작은 공통 다중은 가장 큰 공통 다이서와 가장 일반적인 다중의 관계입니다. 가장 큰 공통 다이서와 가장 일반적인 배수는 단순히 두 가지 개념이 아니라 서로 밀접하게 연결되어 있다는 사실! 알고 있었나요? 둘 사이의 관계는 다음 공식으로 표현됩니다. 위의 공식을 통해, 우리는 가장 큰 일반적인 제수와 가장 공통적 인 배수를 찾는 데 필요한 수학적 아이디어를 요약 할 수 있습니다. 예를 들어 12와 18을 다시 살펴 보겠습니다.

두 숫자의 제품입니다. 가장 큰 공통 구분은 가장 일반적인 다중은 IS입니다. 공식을 확인하면 두 숫자의 제품과 일치합니다! 이 공식은 수학적으로 아름답고 계산 프로세스에 유용 할 수 있습니다. 학습 프로세스를 통해, 우리는 가장 큰 공통 구분과 가장 공통적 인 다중 단계를 찾는 프로세스를 요약합니다. 단계별로 따르십시오! 주요 요인화 사용 방법 : 각 숫자를 주요 요인으로 분해 한 후 일반적인 주요 요인과 각 지수를 비교하여 가장 큰 일반적인 제수 및 가장 공통적 인 배수를 찾을 수 있습니다. 예 : 가장 큰 일반적인 제수는 공통 기본 요인이며 최소 지수는 제품입니다. 가장 일반적인 다중은 모든 주요 요인의 가장 큰 지수의 산물입니다. 유클리드 알고리즘 : 나머지는 0이 될 두 개의 숫자의 가장 큰 공통 구분을 찾기위한 간단한 알고리즘입니다. 이것은 나머지, 나머지, 가장 큰 공통 다이버는 가장 큰 공통 다중입니다. 일반적인 배수 및 일반적인 제단 :이 방법은 초등학생에게 특히 유용합니다. 두 숫자의 모든 요소와 배수를 나열하고 일반적인 부분을 찾는 연습을 통해 직관적으로 이해할 수 있습니다.
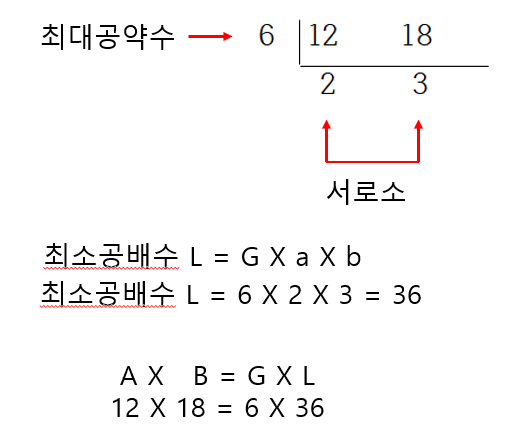
가장 큰 일반적인 구분과 실생활에서 가장 공통적 인 다중 가장 큰 공통 다이버와 가장 일반적인 다중은 수학적 개념 일뿐 만 아니라 실생활에서도 유용합니다! 분수 계산 : 분수를 나눌 때 가장 일반적인 배수를 사용하십시오. 예를 들어, 추가 및 공통 분모로 가장 일반적인 배수를 사용할 수 있습니다. 공정한 분포 : 12 개의 사과와 18 개의 배는 가장 큰 일반적인 구분의 그룹으로 나누어 공정하게 배포 할 수 있습니다. 시간표 생성 : 2주기 가장 일반적인 배수는 일반적인주기를 찾는 데 사용됩니다. 예를 들어, 12 분 일정과 18 분 일정이 동시에 시작되면 몇 분 후에 가장 흔한 일입니다. 가장 큰 일반적인 디바이저와 가장 일반적인 다중이 생각보다 쉽고 유용하지 않습니까? 이 기사가 오늘 당신에게 도움이되기를 바랍니다. 가장 큰 일반적인 제수와 가장 일반적인 배수의 관계를 이해한다면 더 많은 수학 문제를 자신감으로 해결할 수 있습니다!
단계별 맞춤형 학습 프로그램 인 Wink Learning에 대해 알아 보겠습니다.